VEKTOR GAYA DAN RESULTAN SISTEM GAYA
Gaya termasuk besaran vektor. Sehingga pada materi ini kita akan lebih sering menggunakan istilah vektor sebagai pengganti besaran gaya. Karena gaya merupakan besaran vektor, maka sebuah gaya akan ditentukan oleh besar dan arahnya.
Besarnya suatu gaya ditentukan oleh suatu satuan. Dalam SI, gaya mempunyai satuan Newton(N), sedang sistem satuan Amerika menggunakan satuan pound(lb). Arah gaya ditentukan dengan suatu tanda panah.
Gambar 1. Arah Tanda Gaya
A. GAYA PADA BIDANG DATAR
Dua buah vektor , seperti tampak pada gambar 1.2(a) dan (b), yang mempunyai besar dan garis aksi yang sama tetapi arah berbeda, akan memberikan efek yang berlawanan bila bereaksi pada sebuah benda.
Gambar 2. Vektor A
dan bentuk negatifnya
Dua buah vektor P dan Q yang bekerja pada sebuah benda A (gambar 1.3(a)) dapat digantikan dengan sebuah vektor tunggal R yang akan memberikan efek yang sama pada benda tersebut (gambar 1.3(c)). Vektor ini disebut vektor resultan dari vektor P
dan Q.
Gambar 3. Resultan vektor
Dua buah vektor yang besar dan arahnya sama disebut kedua vektor itu sama, tidak tergantung apakah keduanya mempunyai titik aksi yang sama atau berbeda (gambar 1.4). Dua vektor yang besarnya sama, garis aksi sejajar tetapi berlawanan arah disebut kedua tersebut berbeda (gambar 1.5).
Gambar 1.4. Dua vektor yang sama Gambar 1.5. Dua vektor yang berbeda
B. PENJUMLAHAN DAN PENGURANGAN GAYA
Dua buah vektor gaya A dan B bekerja pada satu titik tangkap dan membentuk sudut apit. Resultan atau jumlah kedua vektor tersebut dicari
menggunakan hukum jajaran genjang (gambar 1.6(a) dan (b)).
Gambar 6. Hukum Jajaran genjang
Besarnya resultan dapat dihitung menggunakan persamaan sebagai berikut :
Dari hukum jajaran genjang, dapat diturunkan cara lain untuk menentukan jumlah dua buah vektor gaya. Metode ini dikenal dengan hukum segitiga (gambar
1.7(a), (b), dan (c), gambar 1.8, dan gambar 1.9)
Gambar 7. Hukum Jajar Genjang
Gambar 1.8. Hukum Segitiga Gambar 1.9. Hukum Segitiga
Pengurangan vektor gaya didefinisikan sebagai penjumlahan suatu vektor yang sama dengan arah berlawanan. Gambar 1.10 memperlihatkan pengurangan dua
vektor A dan B.
Gambar 1.10. Pengurangan vektor
Besarnya A-B dihitung menggunakan persamaan berikut ini :
Rumus hukum segitiga yang sering digunakan dalam perhitungan adalah sebagai berikut :
1. Dua buah buah gaya P dan Q beraksi pada suatu paku, tentukan resultannya !








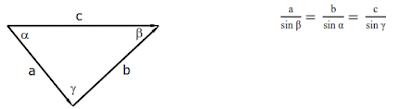



Tidak ada komentar:
Posting Komentar